ガス風船を作るのに必要なガスの量や風船の大きさの数値を「風船の話その1遊び方編」の記事では何の説明もなしに一方的に表示しましたが、ここの記事で具体的にそれらの数値の求め方を説明します。さきの記事では温度や、気圧を固定した条件での数値ですので、利用が限られてしまいます。そこでもうすこし融通がきく数値を求めてみます。ほとんどの方には必要ない知識かもしれませんが、頭の体操だと思ってご覧いただければ幸いです。
熱気球やガス気球の浮力計算のための3つの法則
浮力の計算には3つの法則を使います。
1:アルキメデスの原理
2:ボイル・シャルルの法則
3:アボガドロの法則
この法則をみつけた科学者のイメージ写真をネットから探してみました。
写真①アルキメデス(ギリシャ人BC287?~BC212)
写真②ロバート・ボイル(英国人1627~1691)
写真③ジャック・シャルル(フランス人1746~1823)
写真④アメディオ・アボガドロ(イタリア人1776~1856)
1:のアルキメデスの原理はお風呂の浴槽につかると体が軽くなる現象で、「液体中の物体はその体積と同じ液の重さだけ軽くなる」という法則です。お風呂は液体ですがこの原理は気体でも成り立ちます。
2:のボイル・シャルルの法則は、「温度が一定の場合は気体の体積と圧力は反比例する」というボイル法則と「圧力一定の場合温度が上がるごとに体積が増える」というシャルルの法則を一つまとめた法則です。ボイルの法則は17世紀の発見で、シャルルの法則は19世紀の初めにシャルルが気球に乗って空気をいろいろ観察して見つけた経験法則です。(別々の2つの法則が一つの法則にまとまるのに100年以上かかっているのは興味深いことです。)
3:のアボガドロの法則は「同じ温度のもとで同じ体積をもつ数種の気体が同じ圧力を呈するとき、それらの中には同数の分子が含まれる」という法則です。わかりづらいので解釈し直すと「温度、体積、圧力が同じならばどんな気体も同じ数の分子を持っている。違うのは重さである」ということでしょうか。この法則はそれまでに見つかった気体のいろいろな実験結果で矛盾が生じているので、当時まだ知られていない「分子」というものの存在を仮定し同じ条件(温度、体積、圧力)ならばそのひと固まりの分子は種類によらず同じ数であるという仮説をたてれば、各種の実験結果を矛盾なく説明できるとの主張です。この突拍子もない仮説は発表当時ほとんど受け入れられず、認められるには50年かかったそうです。しかし現在の化学学習で最初に取り上げられる基本法則です。物理学でいえばニュートンの力の法則の「mα=F」(質量m×加速度αが力Fである)に匹敵する基本的な法則です。
浮力の計算をするための各記号の準備
浮力を計算するにあたって、便宜上、温度、体積、圧力、質量を下記のような記号に決めます。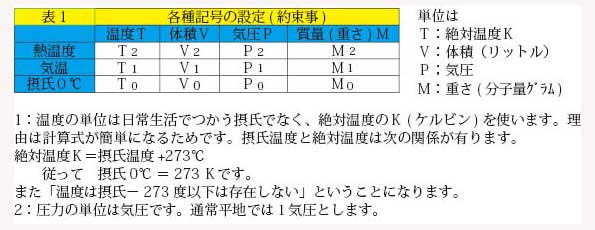
一見して記号の多さに煩わしさを感じるかもしれませんが、計算をするのにはこの方がわかりやすいのです。その理由を説明します。まず表の縦方向で温度Tを0℃、気温、熱温度の3つに分けています。各温度を0状態、1状態、2状態としています。
気温の示す1状態は水素やヘリウム利用のガス気球での浮力計算に使います、熱温度の2状態は熱気球の浮力計算で使います。そして温度0℃の0状態はアボガドロの法則に基づいて計測された、温度、気圧、体積、重さ(分子量)の関係数値が表記してあります。そしてボイル・シャルルの法則によって温度が変化しても気圧や体積の関係が一定であることを利用して、ガス気球や熱気球の浮力を求めることができます。つまり温度が0状態での各要素の数値は計算の元データとして必要なのです。そして温度が0状態での数値は以下の{表2}のような数値になります。重さ(分子量)だけは各元素によって異なるので、{表3}の数値を元にして{表4}で求めています。この{表2}と{表4}の基礎数値を使って浮力が求まります。

水素気球やヘリウム気球の浮力の計算
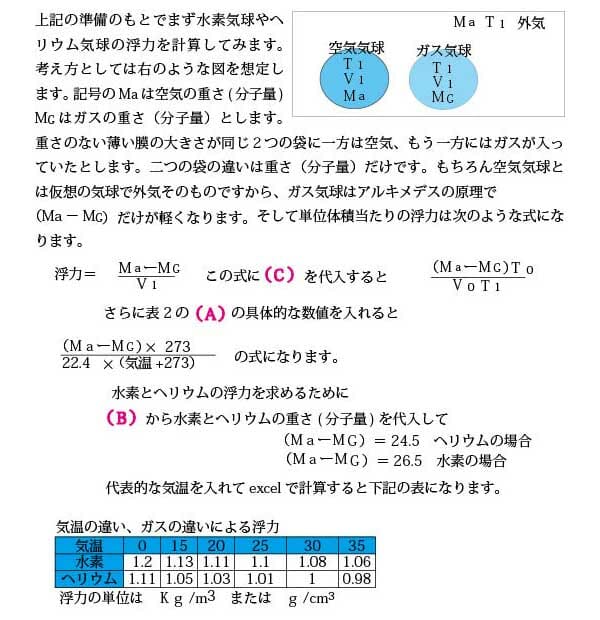
上式に実際の気温と各ガスの分子量を代入すると実際の浮力がもとまります。excelで計算したのが上記の表です。
この表をみると傾向がみえてきます。
1:ヘリウムの浮力は水素より約8%小さい。
2:気温が高いほど浮力は小さくなる。
熱気球の浮力の計算
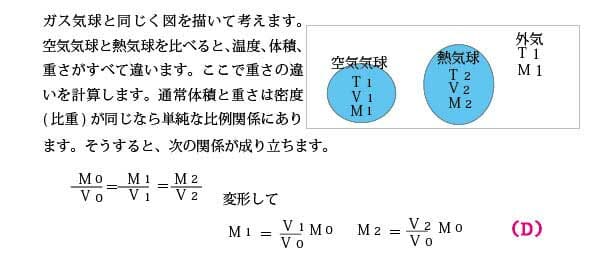


直径16m強の大きな気球を飛ばすというのは当時としては壮大なイベントです。ベルサイユ宮殿前広場に集まった多くの群衆の熱気や歓喜の声が想像されます。今回気球のサイズを机上で計算できましたが、ここで使ったシャルルの法則はこの熱気球のライバルであったシャルルが水素気球を飛ばした後実験を重ねたてできた法則ですし、ましてアボガドロの法則はこれよりさらに50年以上あとに一般認知された法則です。つまり開拓者の人たちは、大した情報もない時代に試行錯誤を繰り返しながら新しい道を開いていったわけです。


